隐性赔率并不难理解，但许多玩家在游戏中误用它们。这会导致一些可以避免但代价高昂的错误，例如追逐不值得追逐的听牌。

为了帮助你避免此类错误，你将要学习什么是隐性赔率，以及它们应该如何帮助你制定策略。我们将涵盖：

• 什么是隐性赔率？
• 隐性赔率是如何起作用的？
• 两个例子，展示了隐性赔率的使用（包括一个可能让你惊讶的场景）

让我们开始吧。

什么是隐性赔率？

隐性赔率是指你期望在后续街道上，如果你击中你的出牌，将赢得的钱的数量。 这个概念与底池赔率结合使用，最常用于帮助你确定用听牌跟注是否值得。

如果你期望在击中听牌后从你的对手那里赢得更多钱，那么你就有好的隐性赔率。但是，如果你预计在未来的街道上无法从对手那里获得更多钱，那么你就有很少或没有隐性赔率。

精确计算隐性赔率实际上是不可能的，因为它需要量化和衡量无数的变量——每张可能的牌、行动、下注额等等，都可能发生在未来的街道上。你所能做的最好的就是用逻辑来估计。

然而，你可以计算的是，为了证明一个原本无利可图的跟注是合理的，你需要在未来的街道上赢得的最低金额。这就是我们将在下一节中介绍的内容。

隐性赔率是如何起作用的？

假设你正在玩一场 1/2 美元的现金游戏，你在转牌圈的位置上持有 K♥ Q♥。牌面是 A♥ 6♦ 2♠️ 9♥ — 给你坚果同花听牌 — 你的对手下注 15 美元到 20 美元的底池中。

一个快速的底池赔率计算（15 美元跟注 /（15 美元下注 + 20 美元底池 + 15 美元跟注） = 0.3）表明你需要超过 30% 的胜率才能盈利地跟注。由于你只有大约 20% 的机会用一张牌击中同花，如果未考虑未来的行动，你将不得不弃牌。

这就是隐性赔率发挥作用的地方。这里有一个公式，用于计算你需要在河牌圈赢得多少钱才能证明在转牌圈跟注是合理的：

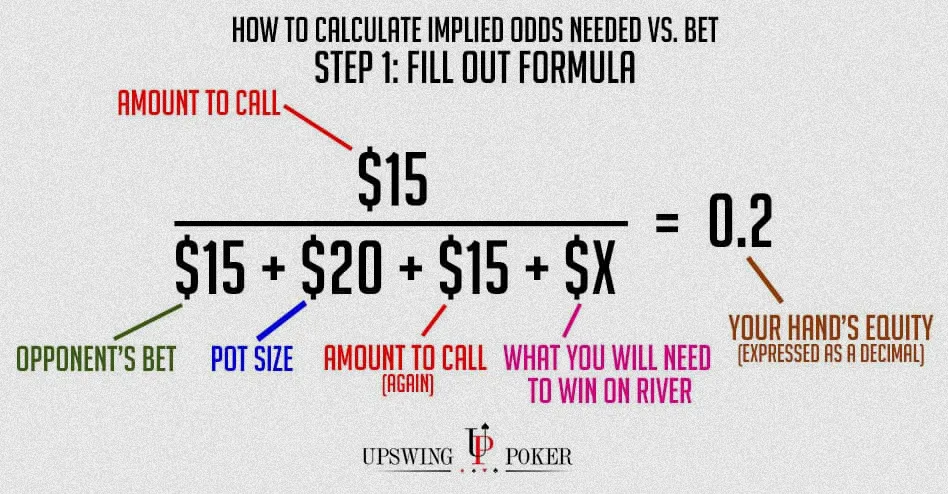
你可能会注意到，这与底池赔率的公式非常相似。唯一的区别是在分母中增加了“X”，以及你的手牌胜率在等式的右边。

现在，让我们求解“X”。

这意味着，当你在河牌圈用 K♥ Q♥ 击中同花时，你需要赢得超过 25 美元才能使在转牌圈的跟注盈利。由于底池已经有 50 美元，你平均只需要在河牌圈提取半个底池的下注。

这个结果似乎是完全可行的，尤其是在同花盖同花的情况下，有可能赢得一个巨大的底池。所以，你应该在这手牌中在转牌圈跟注。

隐性赔率例子

让我们通过几个例子来将这个概念融入你的头脑。系好安全带——这变得有点复杂。

大盲注对按钮位（作为翻牌前跟注者的单次加注底池）

假设你在大盲注位置（OOP）并且是翻牌前的跟注者，持有 J♦ 7♦。你刚刚跟注了翻牌圈的 c-bet。在转牌圈，牌面是 K♦ T♦ 3♠ 2♥，并且你面对来自按钮位玩家的 50 美元下注到 67 美元的底池，该玩家还有 117 美元在后面（你覆盖）。

你的底池赔率是：50 美元 / 167 美元 = 0.3 = 需要 30% 的胜率才能盈利地跟注。

这是你的胜率（用紫色方块突出显示）与一个非常平衡的双重压注范围对抗的结果：

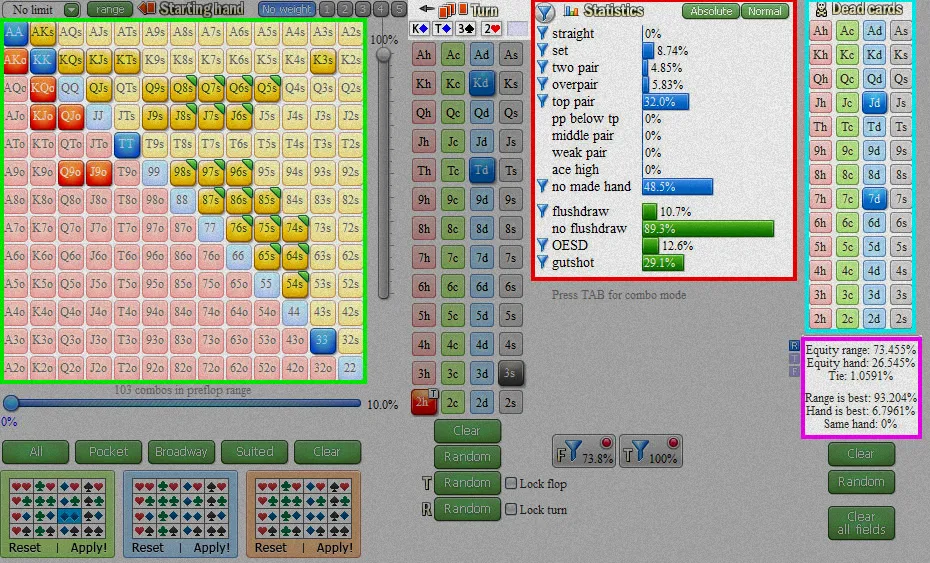
编者注：我们已经为那些不熟悉求解器的人用彩色框突出显示了相关信息。紫色方块 = 胜率。绿色方块 = 对手的估计范围。红色 = 范围统计数据

你可以看到，如果我们只考虑底池赔率，我们就没有足够的胜率来跟注，因为我们只有 26.5% 的胜率。但这只是对情况的不完整评估——我们还没有考虑河牌圈会发生什么。

我们将在河牌圈击中同花的概率是 19.6%——让我们四舍五入到 20% 以简化计算。此外，为了简单起见，让我们假设每次我们在河牌圈击中同花时，我们都会赢得底池（实际上我们大约有 96% 的时间拥有最好的牌）。

现在，我们将使用之前的公式来计算当我们击中同花时，我们需要在河牌圈赢得多少钱才能在我们的转牌圈跟注中收支平衡：

50 / (50 + 50 + 67 + X) = 0.2
50 / (167 + X) = 0.2
50 = 0.2 * 167 + 0.2 * X
50 = 33.4 + 0.2 * X
0.2 * X = 16.6
X = 16.6 / 0.2
X = 83 美元

我们需要在击中后从按钮位赢得 83 美元。河牌圈的底池将是 167 美元，这意味着我们必须提取半个底池的下注才能收支平衡——记住，按钮位后面只有 117 美元。

由于按钮位不会在河牌圈 100% 的时间加注，尤其是在同花听牌击中时，你需要做以下其中一件事才能提取必要的价值：

• Donk-bet（小注）。 如果我们选择这个选项，对手的反应平均必须给我们带来 83 美元。例如，如果我们全压小注 117 美元，按钮位将不得不至少跟注 70% 的时间。
• Check-call（或者如果他下注非全压则 check-raise）。 同样，这平均需要给我们带来 83 美元。例如，他需要至少 70% 的时间全压 117 美元才能在我们的转牌圈跟注中收支平衡。

这些结果是可能的，但没有一个非常可能按照我们需要的方式发挥作用。与 K♥ Q♥ 的例子不同，我们在击中时不会拥有坚果同花，我们处于不利位置，而且没有多少东西可以赢得。所有这些原因使得在河牌圈提取必要的价值变得更加困难。

你可以看到为什么，即使在我们的评估中增加了隐性赔率，我们仍然无法利用这种弱小的听牌盈利地跟注。然而，我们的评估确实表明，它并没有我们之前想象的那么糟糕。

注意：这里的计算被简化，以排除一些因素，即使包含在内，这些因素对结果的影响也很小。这些因素包括在河牌圈击中 J 或 7 并赢得底池，当我们被同花盖牌并输掉很多时，以及当我们被小同花盖牌并赢得很多时。

按钮位对大盲注位（作为翻牌前加注者的单次加注底池）

隐性赔率不仅用于面对带有听牌的下注。当你也是下注者时，它们也很重要。考虑以下情况：

你在按钮位先手加注，并被大盲注位跟注。翻牌是 J♣ 8♦ 5♥。

当您尝试构建你的 c-betting 策略时，你可以考虑你手牌的隐性赔率。为了说明这一点，让我们取两手可能的牌：J♥ 9♥ 和 A♦ J♠。

首先是 J9。这手牌值两个街的价值，所以问题是我们如何提取最大的价值：我们应该在翻牌圈下注、在转牌圈下注、在河牌圈 check，在翻牌圈下注、在转牌圈 check、在河牌圈下注，还是 check 翻牌圈、下注转牌圈、下注河牌圈？

让我们考虑一下当我们改进到转牌圈 9 上的两对时可能出现的场景——对于这手牌来说，这是一个关键的策略转折点：

场景 1： 你 c-bet 并被跟注。转牌圈出现 9。你现在被认为拥有更强的范围，因为 QT、T7s 和 76s 完成了。这意味着你将从你的两对中获得更少的价值，并且当你的对手有 QT 时会遭受反向隐性赔率。

场景 2： 你 c-bet 并被加注。你跟注，转牌圈又是 9。你的对手将经常在这个牌面上加注，因为他的范围由于他的 76 以及 QT 和 T7s 手牌的某些百分比完成而大大提高。你被迫跟注，并且在前进的过程中不会很有趣。

场景 3： 你 check，转牌圈是 9。你的对手现在有大量可能的诈唬手牌，例如 AT、KT、T6s、T4s、T3s、T2s、KQ、Q7s、Q6s、Q4s、Q3s、Q2s 等。他将用这些手牌给你施加很大的压力，因为他的 QT、T7s 和 76 已经完成，你将拿着一手非常强大的手牌在那里跟注他。

你可以从这些场景中看到，check 这手牌是最好的。它通过在对手将受到最强烈攻击的牌上有所改进，在转牌圈表现得非常好。

接下来，让我们看看 AJ。用这手牌，会有一些结果，你可以获得 3 个街的价值，有些你只能获得 2 个街的价值。所以，我们会说这手牌值 2.5 个街的价值。我们如何提取最大的价值？

同样，让我们关注给我们两对——一个 A——的转牌圈，因为这对这手牌来说是一个关键的策略转折点：

场景 1： 你 c-bet 并被跟注。转牌圈是 A。这比大盲注的范围更能提高你的范围，这意味着他会有点不愿意用 8x 和 5x 等手牌进行双下注。无论如何，你拿着一手非常强大的手牌，没有听牌完成，而且你几乎总是能够三桶下注以获得价值。

场景 2： 你 c-bet 并被加注。你跟注，转牌圈出现 A。这张牌比大盲注的范围更能提高你的范围，这意味着他会更加谨慎地诈唬（总的来说）。尽管如此，你的手现在有所改进，可以击败他的一些价值范围，并且没有听牌完成，这意味着你可以轻松跟注。

场景 3： 你 check back，转牌圈是 A。这张牌极大地提高了你的范围，你的对手将以非常高的频率 check。因此，你将从他的诈唬手牌中获得有限的价值。

你可以清楚地看到为什么在这种情况下用 AJ 进行 c-bet 是必须的。所有场景都鼓励立即把钱投入底池。

结论

隐性赔率不仅在你面对下注时很重要；它们在下注时也很重要。它们有助于塑造你的防御和攻击范围，如果你正确使用它们，会对你的胜率产生巨大的影响。正确理解隐性赔率将帮助你更频繁地产生非常容易且有利可图的情况。

今天就到此为止！我希望你喜欢这篇文章，并从中有所收获。像往常一样，如果你有任何问题或反馈，请不要犹豫，使用下面的评论部分。

祝你好运，磨砺者们！

从 Upswing Poker 阅读更多内容：

• Limped Pots：如何调整你的策略以赢得更多钱
• 同花连子：扑克玩家应避免的 5 个策略性错误
• 胜率实现如何影响你将要玩过的每一手牌